Mean, median, and mode are fundamental statistical measures that play a crucial role in understanding data sets. These concepts are not only essential in mathematics but also widely applied in real-world scenarios, from business analytics to scientific research. Grasping the connections between mean, median, and mode can significantly enhance your ability to analyze and interpret data effectively.
Whether you're a student, a professional, or simply someone interested in data analysis, understanding the relationships between these three measures is invaluable. Each measure provides unique insights into the central tendencies of a dataset, and together, they form a powerful toolkit for statistical analysis.
In this article, we will delve into the definitions, calculations, and applications of mean, median, and mode. Additionally, we'll explore how these measures connect and complement each other in various contexts. By the end of this guide, you'll have a solid foundation in mean median mode connections and their practical implications.
Read also:Where Is Michael Schiavo Today Unveiling The Truth Behind The Mystery
Table of Contents
- Defining Mean, Median, and Mode
- Calculating Mean, Median, and Mode
- Connections Between Mean, Median, and Mode
- Real-World Applications
- Data Distribution and Its Impact
- Symmetry and Skewness in Data
- Practical Examples of Mean Median Mode Connections
- Common Mistakes to Avoid
- Tools for Analyzing Mean, Median, and Mode
- Conclusion
Defining Mean, Median, and Mode
Before diving into the connections between mean, median, and mode, it's essential to understand what each term represents:
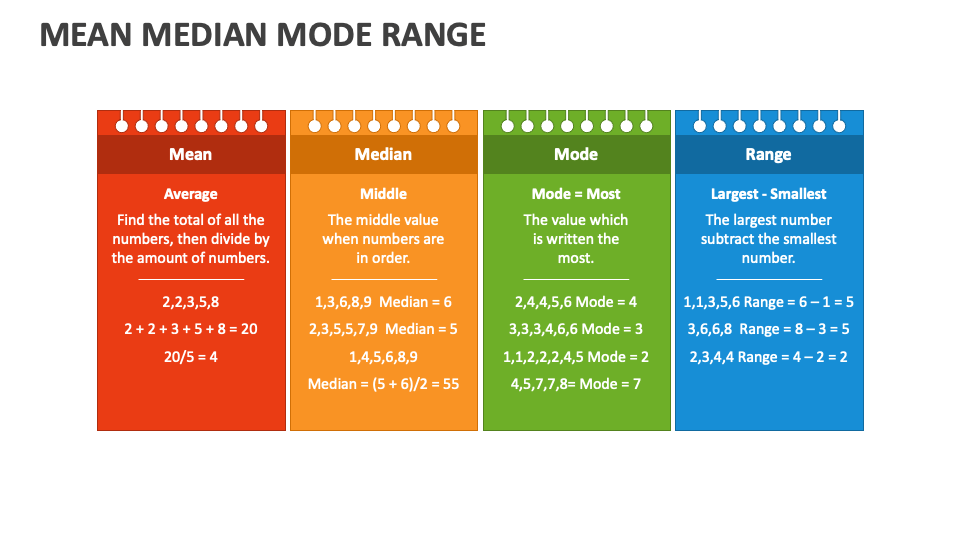
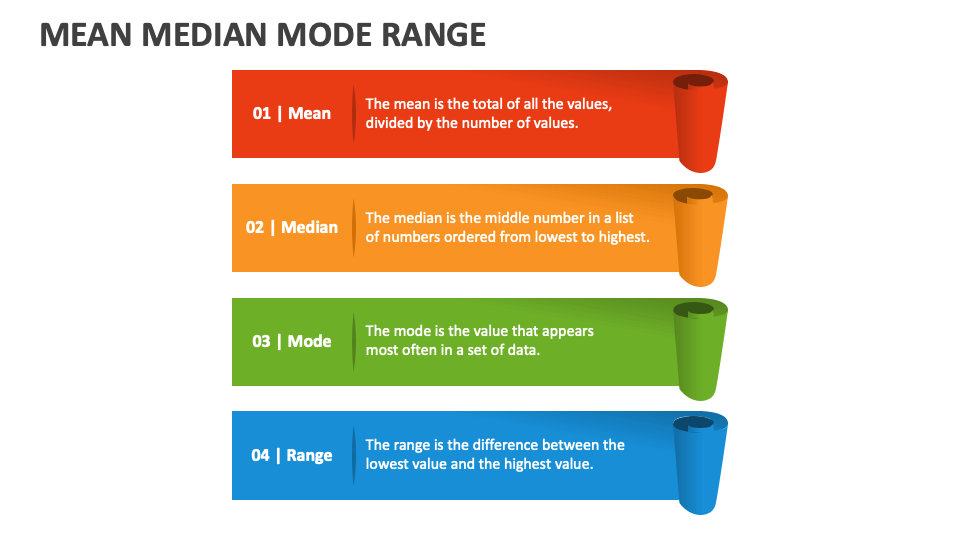
Mean
The mean is the average value of a dataset. It is calculated by summing all the values in the dataset and dividing the result by the number of values. The mean is sensitive to extreme values, also known as outliers, which can skew the overall result.
Median
The median represents the middle value of a dataset when the values are arranged in ascending or descending order. If the dataset has an odd number of values, the median is the middle number. If the dataset has an even number of values, the median is the average of the two middle numbers. Unlike the mean, the median is not affected by outliers.
Mode
The mode is the value that appears most frequently in a dataset. A dataset can have one mode (unimodal), multiple modes (bimodal or multimodal), or no mode at all if all values occur with equal frequency. The mode is particularly useful in categorical data analysis.
Calculating Mean, Median, and Mode
Let's explore how to calculate each measure step by step:
Calculating the Mean
To calculate the mean, follow these steps:
Read also:Otto Kilcher Death A Comprehensive Look Into The Life And Tragic End Of An Iconic Figure
- Sum all the values in the dataset.
- Divide the sum by the total number of values.
For example, consider the dataset: 5, 10, 15, 20, 25. The mean is (5 + 10 + 15 + 20 + 25) ÷ 5 = 15.
Calculating the Median
To calculate the median, arrange the values in ascending order and find the middle value:
- If the dataset has an odd number of values, the median is the middle value.
- If the dataset has an even number of values, the median is the average of the two middle values.
For example, in the dataset 5, 10, 15, 20, 25, the median is 15. In the dataset 5, 10, 15, 20, the median is (10 + 15) ÷ 2 = 12.5.
Calculating the Mode
To calculate the mode, identify the value(s) that occur most frequently in the dataset:
- If one value occurs more frequently than others, it is the mode.
- If multiple values occur with the same highest frequency, the dataset is multimodal.
For example, in the dataset 5, 10, 10, 15, 20, the mode is 10.
Connections Between Mean, Median, and Mode
The relationships between mean, median, and mode provide valuable insights into the nature of a dataset:
- In a perfectly symmetrical distribution, the mean, median, and mode are equal.
- In a positively skewed distribution, the mean is greater than the median, and the mode is the smallest of the three.
- In a negatively skewed distribution, the mean is less than the median, and the mode is the largest of the three.
Understanding these connections helps in interpreting the central tendencies of a dataset more accurately.
Real-World Applications
Mean, median, and mode are widely used in various fields:
Business Analytics
Businesses use these measures to analyze sales data, customer demographics, and market trends. For instance, the median income provides a more accurate representation of a population's financial status than the mean income, which can be skewed by outliers.
Education
In education, these measures help analyze student performance. Teachers often use the median score to assess the overall performance of a class, as it is less affected by exceptionally high or low scores.
Healthcare
Healthcare professionals use these measures to analyze patient data. For example, the mode of a dataset representing patient ages can indicate the most common age group requiring medical attention.
Data Distribution and Its Impact
Data distribution plays a crucial role in determining the relationships between mean, median, and mode:
- A normal distribution is symmetrical, and the mean, median, and mode coincide.
- A skewed distribution affects the relative positions of these measures, providing insights into the dataset's characteristics.
Understanding data distribution helps in selecting the most appropriate measure of central tendency for analysis.
Symmetry and Skewness in Data
Symmetry and skewness are key concepts in data analysis:
Symmetry
A symmetrical distribution is one where the data is evenly distributed around the central value. In such cases, the mean, median, and mode are equal, making it easier to interpret the data.
Skewness
Skewness refers to the asymmetry of a distribution. Positive skewness indicates a longer tail on the right side, while negative skewness indicates a longer tail on the left side. Skewness affects the relationships between mean, median, and mode, providing additional insights into the dataset.
Practical Examples of Mean Median Mode Connections
Let's explore some practical examples to illustrate the connections between mean, median, and mode:
Example 1: Income Analysis
In a dataset of household incomes, the mean income might be higher due to a few extremely wealthy individuals. However, the median income provides a more accurate representation of the typical household's financial status.
Example 2: Test Scores
In a class of students, the mode of test scores might indicate the most common score achieved, while the median score represents the performance of the middle student.
Common Mistakes to Avoid
When working with mean, median, and mode, it's essential to avoid common pitfalls:
- Over-relying on the mean without considering its sensitivity to outliers.
- Ignoring the context of the data when interpreting the median.
- Failing to account for multiple modes in a dataset.
Avoiding these mistakes ensures more accurate and meaningful analyses.
Tools for Analyzing Mean, Median, and Mode
Various tools and software can assist in analyzing mean, median, and mode:
- Excel: A widely used tool for calculating these measures and visualizing data.
- R and Python: Powerful programming languages for statistical analysis and data visualization.
- SPSS: A statistical software package commonly used in social sciences.
Utilizing these tools can enhance the accuracy and efficiency of your analyses.
Conclusion
In conclusion, understanding the connections between mean, median, and mode is crucial for effective data analysis. Each measure provides unique insights into the central tendencies of a dataset, and together, they form a comprehensive toolkit for statistical analysis. By considering factors such as data distribution, symmetry, and skewness, you can interpret data more accurately and make informed decisions.
We encourage you to apply these concepts in your own analyses and explore their practical implications. Don't forget to share your thoughts and experiences in the comments below. Additionally, feel free to explore other articles on our site for more insights into data analysis and statistics.